Review: Style Transfer

Contents

• Introduction
• At The Beginning, There Was Computer Graphics
• First Revolution: Computer Vision
• Second Revolution: Deep Learning
• Summary

Introduction

Style transfer refers to a class of methods that transfer the “look and feel” of a reference style (target) to some other images or videos (source). The definition of “look and feel” here is somewhat flexible. It can be the brushstrokes and the pigments of a painterly image¹, textures compose a modern art², the color scheme of a landscape photo³, or even the movement of a dancing person⁴.

As diverse as the styles can be, the “content” of the source has to be preserved, such that the identity of the object or person has to be kept unchanged even its appearance has been “re-rendered.”

Style transfer is right at the convergent field of computer graphics, computer vision, and machine learning. It is the perfect combination of science and art: A full-stack understanding of visual data is required to analyze the problem and synthesize convincing results. Once works, it produces results of unmatched visual joy. It covers a broad range of technical topics: image processing⁵, features extraction and analysis⁶, segmentation⁷, texture synthesis⁸, parameteric⁹ and non-parametric¹⁰ models, optimization¹¹, and of course nowadays red-hot machine learning such as autoencoders¹², generative models¹³, unsupervised learning with GANs¹⁴ etc.

This article aims to give you a comprehensive overview of this exciting research topic. The timeline of research development structures the content: We will first review the early work in this area, which are computer graphics methods that emulated artistic materials. As visually plausible as the results are, these methods are rendering techniques that required a significant amount of human intervention. We then fast forward to the early 2000s, where new techniques were invented by combining computer vision with computer graphics, and fully automatic example-based image synthesis started to become popular. Techniques in this period laid the foundation of nowadays’ style transfer techniques. We will focus on the problems of color image editing, non-photorealistic rendering, and texture synthesis because many of today’s techniques can be traced back to these ideas. Having understood the past techniques, including their strength and limitation, we will dive into the recent development in the deep learning context. Like many fields in computer science, the landscape of style transfer technique has been entirely reshaped by deep learning in the past few years (As the writing of this article, I meant 2016 - 2018). We will have a journey through the seminal works in this period and understand why we are able to see what we see today in style transfer.

So buckle up, let’s begin the magic carpet ride of style transfer!

At The Beginning, There Was Computer Graphics

Early style transfer researches focused on computer graphics algorithms that emulate particular media in artworks. For example, hairy burshes¹⁵, oil paint¹⁶, watercolor¹⁷, curved brush strokes¹⁸, Impressionism¹⁹, pen-and-ink²⁰. One good example is the Computer-Generated Watercolor¹⁷ method invented by C J. Curtis et al., which use fluid simulation to generate interaction between the pigment, the water, and the paper.

One common problem for these emulation based methods is their slow speed. In particular, it is non-trivial to parallel these methods for realtime rendering. Luckily, computer graphics is all about producing a visually plausible effect in affordable ways. If this is the end goal, there is room for deviating from real-world physics and “hack” effects that look good on screen. One good example is the Fast Paint Texture¹⁶ method developed by A. Hertzmann. Instead of simulating how oil interacts with the canvas, simple textured height map and bump-mapping are used to produce a convincing oil-paint stroke effect. This “trick” allows brush strokes to be synthesized at realtime for human interaction.

Another common problem is the requirement of human intervention, which made these methods infeasible for automatic style transfer. A good example is the Paint by numbers²¹ method developed by P. Haeherli, which requires a user to select the location of each brush as well as its shape, direction, and size. Several follow-up works²⁰ made the interactive process semi-automated, for example, by orienting the brushes based on the underlying image gradients. However, fully automatic style transfer can not be achieved without a sophisticated understanding of the image. In particular, emulation based methods can not answer the question of how to separate the content from the style, nor how to combine the style with new content.

Beyond time complexity and lack of autonomous, it is also very expensive to design algorithms for every new style. In general, formulating mathematical definition for the “look and feel” is a very hard problem. The field needs a universal way to capture arbitrary styles automatically.

In summary, there are three main unsolved problems in the early days’ style transfer: speed, automation, and generalization. Since then, the field experienced two major revolutions. First time in the early 2000s, triggered by the advancement of computer vision techniques. We are now at its second revolution that triggered by the renaissance of machine learning began in 2011.

First Revolution: Computer Vision

Computer vision is about extracting useful information from visual data – a mapping from image to model. It is opposite to computer graphics, which models the mapping from data into images. Around the early 2000s, researchers started to realize that by combining vision and graphics, one can have a complete pipeline that first extracts useful information from an image, then use the information to control the generation of new images. This technique is called “example based rendering”, and it revolutionized the field of style transfer.

Among the numerous researches carried out in this period, we pick the three most relevant categories to discuss: color image transfer, non-photorealistic rendering, and texture synthesis. These methods have a strong connection to the techniques we are developing today. By knowing the past, we can understand the origin of the story and the principle ideas that used to drive the field forward. By knowing the past, we will also understand the limitation of these classic ideas and the significance of the work we do today.

Colour Image Transfer Some of us have the experience of the color editing tools in programs like GIMP or Photoshop.

“One of the most common tasks in image processing is to alter an image’s color.” – Color Transfer between Images²², E. Reinhard et al.

Sometimes it can be tedious to figure out the best color, brightness, and saturation of a photo. One of the earliest style transfer methods²² is invented to address this problem: why not just select a reference photo that looks good, and transfer its color scheme to the photo that needs editing. The color scheme of an image is modeled by three Gaussian distributions, one for each image channel. To transfer the color scheme from one image (target) to another (source), they simply re-normalized the Gaussian distributions of the source image so they matched the ones in the target image. Notice that the normalization is performed independently to each of the three channels. For this reason, it is helpful to de-correlate the color channels before normalization (map the RBG values into the $l\alpha\beta$ space).

One interesting discovery of this study is that global transfermations in the colour feature space (either RBG or $l\alpha\beta$) preserve the image content very well. We will see this phenomenon, together with the ideas of feature decorrelation and Gaussian parameterization, also thrive in later deep leanring based methods²³,²⁴.

Non-Photorealistic Rendering Non-photorealistic rendering (NPR) refers to a class of rendering techniques that pursues stylization over realism. Here we only briefly discuss the major categories in this field. Please refer to this comprehensive survey paper²⁵ to know all state of the art NPR techniques before the deep learning renaissance.

Image processing, especially local filtering techniques, provide a promising alternative due to parallelizing these methods are straight forward. For many years, researchers handcrafted better and better filtering techniques. One of the seminal work in this category is Video Abstraction by Winnemöller et al.²⁶. Their pipeline first uses the bilateral filtering to perform edge-aware image smoothing, then a difference of Gaussians (DoG) filter is used to detect salient edges. The smoothed image and the edge map is combined and quantized to achieve a stronger effect. The downside of this category of work is it is difficult to extend the visual effect beyond the cartoon-like style, due to the limitation of handcrafted low-level image filters. Luckily, as we will see, this limitation will be lifted by a learning-based method and deep neural networks’ cascaded nonlinear processing.

Apart from image filtering, segmentation²⁷ also helped non-photorealistic rendering. D. DeCarlo et al.²⁸ first segment images in a scale-space pyramid. The salient regions in the image are locally decomposed into finer segments traversing the pyramid. Outlines of the regions are smoothed and superimposed to delineate region boundaries. The result is a line-drawing style using bold edges and large regions of uniform color. Segmentation method has also been used to improve temporal coherence²⁹,³⁰ in video style transfer, or producing a unique style that is composed of abstract shapes³¹.

One NPR researcher that is worth special mention is A. Hertzmann. Among many of his highly cited publications³²,¹⁸, Paint By Relaxation³³ is the first method that frames style transfer as an optimization problem. In particular, this work formulates a combination of multiple energies to strike a good trade-off between the content and the style: the desire to closely match the appearance of the source image (content preservation), and the desire to use as few strokes as possible (stronger abstraction, more stylish). With retrospect, this is significant as the first working proof of optimization for style transfer.

Unfortunately, these methods are not versatile in terms of depicting styles. They produce fantastic results for oil paintings and cartoon-like style but are difficult to generalize to a wide variety of styles.

Texture Synthesis

Texture synthesis is a widely used technique in computer graphics. The Markovian property of texture makes it possible to algorithmically constructing a sizeable digital image from a small digital sample image. In the context of style transfer, texture synthesis is significantly more flexible than handcrafted NPR methods: the “style” is encoded in the target example and does not need any handcraft.

We have the seminal works from A. Efros et al. ³⁴ and A. Hertzmann et al.³². Both of these works are published at Siggraph 2001 and address the problem of example-based texture transfer: rendering an image with a texture taken from a reference style image. The key idea to find correspondence between the source image and target image, and copy the best-matched content (pixel or patch of pixels) from the target image to the source image. The copied content is either blend or stitched to form the final image.

One of the critical challenges is how to find good correspondence between two very different images. Both of these two methods proposed to match the low-passed filtered image, intending to reduce the influence of texture and make the match ground more on context. However, such pixel-based matching can still be unreliable.

Another critical challenge is how to blend the copied content into an image. Simple overwriting or averaging overlapped pixels lead to artifacts such as ghosting and blur. A better way is to stitch patches together using boundary cut (dynamic programming³⁴ or graphcut³⁵). It allows a smooth transition between the boundary of different patches. However, it is not guaranteed that the optimal cut always leads to a good result. In many cases, it is simply impossible to have a visually seamless solution.

Even though there are such limitations in pixel space, these style transfer methods still produced some mind-blowing results. They are a solid baseline to compare with the new deep learning-based approaches. Many of today’s texture transfer can be seen as extensions of these ideas to deep learning domain. As we will discuss in details, with deep features, both patch matching, and patch blending are more reliable.

Second Revolution: Deep Learning

Many of us know about the story of how AlexNet made deep learning famous almost in one night by its stylish win of 2011’s ImageNet challenge. But fewer know the first killer App of deep learning actually happened a lot earlier than that. It is the Hinton and his students’ 2009 work in Speech Recognition showed the world the first time that with enough data and enough computation resource. Since then, it was just a matter of time for deep learning to reshape the landscape of many research fields. Style transfer was no exception.

Before diving into the (deep) learning-based method, let us do a little summary for the journey so far:

1. On the bright side, we witness the value of both parametric (color image transfer) and non-parametric (texture transfer) model for style transfer. The parametric model, for example, fitting Gaussian distributions to pixel values, is a simple but effective way of transferring color. The non-parametric model, such as the Markov Random Fields, has found its usefulness in texture transfer. Image filtering has excellent success in rendering a particular cartoon-like style. We will see all these ideas will continue to shine in the deep learning era.
2. On the other side, let us exam what went wrong. What went wrong was all these methods are executed in pixel space (individual pixels, a local patch of collection of pixels, distribution of pixel value in color space). Such a low-level representation has led to the significant limitation of pre deep learning-based style transfer techniques. Precisely, pixel-based representation can not capture complex image statistics, let alone the semantics. Hence the model built upon such representation can’t fully capture neither the content nor the style.
3. In the meantime, there is a lack of learning process in all these methods. They are either handcrafted (image filters) or single example-based method (color transfer, texture transfer). The reason might well be it is difficult to learn anything powerful in the pixel space.

Having these observations in mind, let’s continue the journey into the land of deep learning, which in essence solves the representation problem and the learning problem.

Deep Visualization The main reason that deep features are better than pixels is that they encode more useful image statistics at multiple scales. Remember the days when image filters are handcrafted? Learning these filters from data is a million times more powerful and efficient.

Deep learning and image generation was first bridged by visualization techniques ³⁶,³⁷,³⁸,³⁹ that were initially invented to make the network more interpretable. One particular type of visualization method uses backpropagation to “reconstruct” an input image from its deep feature encoding. Notice, in this case, the weights of the networks are frozen, the backpropagation modifies only the feature activation to update the input image.

For example, it can generate an image that would give a high probability of a particular object class (the final output of the neural networks). It can also create an image that leads to activation in intermediate layers. Such a general framework for inverting a representation paved the way for deep feature-based image synthesis – whenever you have a deep representation, getting an image out of it is straight forward.

In the context of style transfer, the first milestone visualization of deep features is probably Deep Dream⁴⁰. It starts off using the backpropagation inverting technique³⁷, but add a smart twist to it: instead of simply inverting the feature activations, it amplifies them. That means, whenever the neural network seems an exciting pattern or object, the input image is changed in the way that the neural network can see more of it. Formally, this is achieved by using the feature activation as the gradient to backpropagation. The results of Deep Dream can be seen as one particular type of style transfer, where the style are the image statistics encode in the network’s weights. This leads to very intensive stylization results, almost feels like the dreams made by the networks.

One limitation of Deep Dream is the lack of controllability. Although it is possible to manually specified what filters to amplify, transfer a particular style, such as one of Van Gough’s paintings, is not possible. To do that needs non-trivial reverse-engineering the style in deep feature space. Our next stop is such techniques that formulate style objective using deep features and use such objectives to drive the representation inversion towards a stylish image.

Parametric Neural Style Transfer

Remember the color image transfer²² which parameterizes per-channel Gaussian distributions to represent the color scheme in an image; parametric methods are invented to generalize such techniques to deep feature space for style transfer. In particular, Gatys et al.’s 2016 paper was the first to implement this idea successfully. This seminar paper coined the term “neural style transfer”. Since then, there have been hundreds, if not more, followup works. All these works can be roughly categorized into three divisions based on the different aspects of style transfer they improved: quality, speed, and versatility.

Quality: Let’s begin with Gatys et al’s seminar paper. The key insight of this work is the formulation of style as the distribution of deep feature activations. The problem of style transfer then boils down to aligning such distribution computed from a source image to the distribution computed from a target distribution.

Precisely, the gram matrix of feature activation as a particular layer is used to characterize the style (mainly textures) at a specific scale. Multiple gram metrics from different layers capture the style at multiple scales. We will come to why gram matrix is a good representation for style in a bit. Now, to transfer the source image towards a target style, the deep feature representation of the source image is inverted back to an image using the backpropagation method³⁷ with an additional style criteria that minimizes the L2 distance between the gram metrics of the target style and the gram metrics of the stylized source image. Without the style loss, the inversion would lead to a faithful reconstruction of the input source image. With the style loss, the inversion is driven towards the style in the target image²³.

There are some non-trivial observations can be made in this work and in some the followup works:

1. Deep parametric representation with simple statistics works really well for some textures. The heart of Gatys et al.’s neural style method is the gram matrix. Research was made to prove that in essence such a gram matrix capture Maximum Mean Discrepancy (MMD) with the second-order polynomial kernel⁴¹. At the same time, the same reseach observed that using the gram matrix is not mandatory. In fact, the key of neural style transfer is to match the feature distributions between the style images and the generated images, and everal other distribution alignment methods, including covariance matrix²⁴, can also achieve appealing results.
2. It is also interesting to see that merely inverting deep feature with both the content loss and style loss often lead to satisfactory results. Considering this: there is no guarantee that the inverted image has a plausible appearance, except for it needs to satisfy some constraint made in the deep latent space. The fact this works well indicates that the backpropagation process must have some strong regularization that prevents the generated image from going crazy. This is very likely to due to the transposed convolution operation which acts upon the image statistic encoded in the VGG network.
3. One catch is that it works a lot better is a second-order optimization method (L-BFGS⁴² in this particular case) is used for updating the result. The results of first-order optimization methods (SGD, momentum SGD, or Adam) seem to get stuck in local optimal quickly. In contrast, L-BFGS does not only arrive the convergence a lot faster but also gives better results. This suggests that second-order optimization methods do have a particular advantage if the exact energy landscape can be fit into the GPU memory. In this case, the optimization only concerns a single image, so the target objective is definite.
4. It is not clear that aligning the distribution towards the style reference image is always a good idea, especially in cases where simple statistics cannot accurately approximate the distribution of the features. For this reason, style decomposition⁴³ is proposed to better model the subtle style differences within the same style image and then use the most appropriate sub-style (or mixtures of sub-style).
5. Cross-layer gram matrices⁴⁴ are proposed to improve the visual quality of the results. The method produces large, principled improvements, particularly for styles where inter-scale relations are important.

Speed: One of the directions orthogonal to image quality is speed. The original neural style²³ needs hundred of iterations to converge. Putting this in aspect, it takes approximately to 1-2 minutes for a Titan XP card to stylize a 1024x720 size image. This put the method firmly at the low-speed category and makes it infeasible for applications such as real-time style transfer for videos.

The most time-consuming part of neural style²³ is the iterative optimization step. To speed up the technique we need to replace this part by something faster. One option is using a feedforward autoencoder to approximate the iterative optimization. Intuitively, the autoencoder learns a nonlinear mapping from source images (in most case, real-world photos) to the look and feel of a target style (usually, artworks). The encoder part of the networks extract the semantic of the source image, and the decoder part of the network re-render the semantic with a new appearance (texture). To train such a network, the same content loss and style loss from ²³ is used. Seminal works in this category include J. Johnson et al. ‘s feedforward networks trained with the perceptual loss⁴⁵, and D. Ulyanov et al. ‘s Texture Networks⁴⁶. The results are further improved by instance normalization⁴⁷, which replace the normalization with batch statistics by normalization with image statistics. The insight of instance normalization is such that because there is a fixed style target (the distribution of the features from the reference style image) for all inputs, it is helpful to normalize each input feature activation independently to a fixed input distribution (subtract the mean of individual image, and scale by its standard deviation). Then learning a mapping from the fixed input distribution to a fixed target style distribution is easy. In contrast, batch normalization will first map each image to a different distribution based on the batch statistics, which makes the transfer to the fixed style target distribution a lot harder, and leads to sub-optimal results (weak style, diffused texture, etc.).

One separate concern raises when applying fast style transfer to video – the temporal coherence. Networks learned to transfer single image independant from each other will generate flicker artifacts to video. This problem was known even at the earlier vision based approaches. Volumetric segmentation was used in those early works to improve the temporal coherence. Methods are also proposed to address this problem in the context of deep learning. The “real-time neural style transfer for videos” method⁴⁸ from Huang et al is one of the earliest work in this regards. During training, the authors add an additional temporal loss to penalize the difference between pixel values of two consectively stylzied frames. The first stylized frame is warpped by optical flow pre-computed on the un-stylized frames. In this way the network is able to minimize the flickers in the output.The similar idea is implemented by concurrent works⁴⁹,⁵⁰.

Versatility Another direction that is orthogonal to both quality and speed is versatility – precisely, how universal is the method to cope with different target styles. To this end, the pre-mentioned feedforward methods⁴⁵,⁴⁶ are limited to a single target style. More precisely, the networks must be retrained for each style, make it expensive to train and store in practice.

Making the technique more versatile is hence of paramount importance. Wouldn’t it be nice to have one network that is capable of multiple styles, or even all possible styles? Actually, there has been some very exciting work⁵¹,⁵²,⁵³ that address this question, among which we will discuss the “whitening color transformation” method in details due to its supreme versatility and mathematical elegance. The idea turns out to be very similar to the early color image transfer²² method, which first decorrelates the pixel value in color space and then applies a global translation and scale operation to align the per-channel color distribution of the source image toward to the target image. In the case of WCT, there is also a feature decorrelation process (whitening operation) and a transform process (coloring operation). The difference is that these operations are applied in deep feature space with computation of the covariance matrix²⁴, as opposed to some pre-defined perceptual transformation in the pixel space. In practice, this turns out to be a very good way of transferring style. The technique is also universal to arbitrary styles: there is no need to train for each style, only a general autoencoder(trained with image reconstruction loss) is needed to compute the deep features. Then style transfer is as simple as decomposing the covariance matrix of the features of the style image.

WCT hit a good balance among quality, speed, and versatility. In a recent follow-up work, the method is further improved from the speed aspect by replacing the relatively more expensive matrix decomposition by a neural network approximation⁵⁴.

Before we move to the Non-Parametric method in the next chapter, it is worth mentioning that the parametric method never worked well in the classical texture synthesis methods, due to its lack of express power in pixel space, and frequently distortion. This, however, is not a big problem for style transfer in deep feature space. One interesting perspective is high-dimensional features (after non-linear transformed) are easier to be modeled by simple statistics. For example, distributions of different classes of objects are more linearly separable in deep feature space. It is interesting to see that such property helped parametric methods to shine in the field of style transfer.

Non-parametric Neural Style Networks One natural extension of the classific non-parametric texture transfer method is to apply it with deep features. This stream of methods have very different characteristics from previously discussed parametric methods.

The first non-parametric neural style transfer is the CNNMRF⁵⁵ method proposed by C. Li et al. It is a straight forward extension of the classical non-parametric texture synthesis methods¹⁰ to the deep neural networks domain. CNNMRF recognizes that deep feature maps in neural networks can also be modeled as Markov Random Fields, where a neural activation only depends on its surrounding neighbors. The advantage of using deep features is they allow semantic-based patch matching, which is way more robust than the pixels-based patch matching. At the same time, blending “neural patches” can leverage their semantics and can be easily inverted to the pixel space. The results are usually better than directly patch blending or stitching in the pixel domain, thanks to the rich image statistics encoded in the deep neural networks. In general, CNNMRF can handle more challenging texture transfer than conventional pixel-based methods. Compared to optimization-based non-parametric Neural style²³, CNNMRF produces better results in transferring miso-structure from the target style, for example, shapes and photorealistic textures. On the other hand, its lack of flexibility for painterly textures such as brush strokes and require stronger similarity between the source image and target image to get a successful transfer. Another interesting extension of classical non-parametric methods is the Deep image analogies method⁵⁶, which analyzes the similarity between a pair of images and then transfer texture from one to another. Different from the original image analogies method from A. Hertzmann, deep image analogy have a more robust matching and blending with deep features. Compared to CNNMRF, it also employs a stricter constraint during feature matching and transfer. In CNNMRF, the neural patches are matched and blended independently at different layers, which has led to artifacts at regions that contain inconsistent matching across different layers. In particular, correspondence between two adjacent layers cannot be exactly maintained due to non-linear modules in CNNs (i.e., ReLU, Max-Pooling). To address this problem, deep image analogies transfer the texture layer by layer: it first transfers the feature maps at a higher layer before deconvolving the warped features for the next layer. In this way, texture transfer in the lower layer is guided by the results in the upper layer.

Effort has also been made to combine non-parametric and parametric approaches. For example, a parametric loss (the mean and covariance matrix of feature activations) is combined with a non-parametric loss in the Optimal Transpor tNeural Style method⁵⁷. In particular, the non-parametric model in this work is a relaxed Earth Mover Distance (EMD) between the content and style feature activations. This is similar to methods like CNNMRF, but differs in one major way: The feature matching in CNNMRF is single-direction from the content image to the style image. This means features of the output image do not need to cover the feature distribution in the style image. In contrast, the relaxed EMD is a bidirectional matching that also encourages covering the feature distribution in the style image. For this reason, the Relaxed EMD tends to produce richer style effect in its results.

Histogram matchig⁵⁸ is also invented to solve a particular artifact (under-saturated regions) in the transferred results. The authors argue that such artifact is caused by the ambiguities in the gram matrix as a mean to model the distribution of feature activations. For example, two very different distributions can have the same gram matrix, which means the optimization can find a solution that is numerically optimal but visually unsatisfactory. To avoid this, histogram of feature activation on a particular layer is computed. Precisely, the feature map is flattened into one dimensional vector so all activations across all channels are jointly modeled. Then, the histogram of the content image is matching to the histogram of the style image, so the order and the magnitudes of the features activation are changed towards the style image. By combining this histogram loss with the original gram matrix loss, the output image is less likely to have under-saturated artifacts.

Efforts are also devoted to making the non-parametric method faster for realtime performance. Similar to the fast parametric method, a feed-forward network can be applied here. The Fast style swap⁵⁹ method trained a decoder network that can directly inverse the style swapped feature map (VGG10 features) to an image. During training, the decoder network is fed with realphotos, artworks, as well as pre-stylized images using the slow opitimization method. The use of pre-stylized images during the training allows the decoder to see stylized input feature maps. Apart from speed, this method is able to uinversally work with new, unseen style image, due to the ability to inverting arbitary images.

In general, parametric and non-parametric methods complement each other. However, non-parametric methods are more effective in classical pixel space due to, and parametric methods are more popular in deep learning time due to the fact deep features are more powerful and easier to be modeled with simple statistics.

Generative Adversersial Networks

Both parametric and non-parametric style transfer has produced some fantastic results. However, there are still many questions unanswered.

The first item on the list is the distance metric for measuring the similarity between the source and the target. Parametric methods, which use global statistics of feature activations, tend to be too flexible. In consequence, these methods often lead to distortions. While such artifacts may not appear to be a big problem for painterly textures, they clearly can harm regular patterns or photorealistic textures. On the other hand, non-parametric methods rely on matching and copy features based on L2 norm or correlation. These method are less likely to produce distortions but at the cost of being too rigid for transfering painterly texture. Such rigidity also imposes the limitation of requiring stronger semantic similarity between the content-style pair.

So the question is, is there a better metric that is neither too flexible nor too rigid, so work well on both non-photorealistic and photorealistic style transfer?

Another question is how to learn the style at scale. All previously mentioned methods learn the style from a single image. Even in the universal style transfer case, the output is modulated by a single image. What if we want to find the characteristic of an artist, or a collection of artists? For example, what makes Monet’s paintings look like Monet’s painting? It is necessary to look for a more generalizable learning approach if we want to push towards this direction.

To be clear, these are very hard questions. Only a decade ago, probably few would dare to predict this will ever be sucessful. Although it is still far from being solved, the research community have made significant progress based on a piece of new learning algorithm called “Generative Adversarial Networks”, or GANs. And in this chapter, we will discuss this method in the context of style transfer.

GANs¹⁴ is a method that simultaneously learns two things: First, it learns to recognizes discrete samples from a distribution; Second, it learns to sample new data from the distribution. To do so, GANs use two networks: First, a discriminator for classifying whether a sample comes from the target distribution or not. This corresponds to the learning of recognizing samples from the distribution. Second, a generator that produces new, unseen samples from the learned distribution. This corresponds to the learning of how to sample from the distribution. These two networks are learned jointly using a min-max game, where the discriminator learns to seperate real data from the generated data, whereas the generator tries to produce data that can fool the discriminator. The goal is, by the end of the learning, the generator is so good that the discriminator can no longer distinguish between which the data produced by the generator and which are the real sample.

The discriminator is typical MLP or convolutional nets that computes the probability of whether an input is real. The generator takes discrete samples drawn from a simple probability distribution, such as an uniform random distribution or a gaussian distribution, then use a MLP or convolutional nets to transfer the sample to an aribitrarily complext target data. In essence, the generator acts as a powerful non-linear mapping from the input distribution to the target distribution.

So why is GANs relevant for style transfer? Well, the generation of images with a particular style can be thought as a process of sampling data from the distribution of the style features. The implication of GANs in the context of style transfer is that the learnt generator can approximate the process of sampling from a distribution – there will be no need to explicitly write down the math of this distribution, nor there is any need to use copy discrete samples.

Precisely, to learn the style of a single painting, or a collection of paintings, or even a collection of artists, we simply treat these examples (image patches in the painting in the first case, or individual artworks in the other two cases) as discrete samples drawn from the target distribution. The generator can generate new patches or new artworks that appear to be valid samples from that distribution. The discriminator acts as an universal metric for measuring the similarity between the style and the output. No handcrafted metrices anymore!

There is one more trick to make GANs work for style transfer: instead of taking random input, the generator takes the source image as the input and usually has a autoencoder-like architecture. The encoder encodes the source image to a latent representation, and the decoder decodes the latent representation to a stylized output. In this way, the generator learns to map the source image to the target style. Another way to think about it is to make the generator conditioned on the latent representation.

One of the earliest work to apply GAN in style transfer is the Markovian GANs⁶⁰ from C. Li et al.. The authors first proved that using the discriminator in GANs can replace Gram matrix for style transfer in an optimization based setting. They then train a generator (feed-forward autoencoder) jointly with the discriminator for fast style transfer. Similarly, CycleGANs⁶¹ use GANs on image patches and can amazingly transfer both photorealistic non-photorealistic styles. To do so, a collection of related images are used during training for better generalization performance. For example, paintings from the same artist, or landscape photos took in the same season. The authors also invented the cycle loss to address the under-constrained in training GANs with unpaired data. In a follow-up work⁶², the other improve the conditional GANs for transferring photorealistic texture to semantic labeling maps or contour images and allow interactive user editing.

In general, GANs has a clear advantage in transferring photorealistic texture in comparison with the non-parametric and parametric methods. It is easy to see that the generator in GANs is very similar to the autoencoders in the previous methods. So the gain must come from somewhere else. One important reason could be that the adversarial learning of discriminator avoids direct style copying and handcrafting style representations. Another possible reason is the ability to learn style from a collection of images (as opposed to learning from a single image) allows the generator to generalize better.

Summary

This article gives an overview of the past and current progress in the field of style transfer. We first review the landmark works in the pre deep learning literature and drawn conclusion the pros and cons of different techniques, including color image transfer, emulation based non-photorealistic rendering, image filtering, and texture synthesis/transfer. We highlight the key insights of these techniques, for example, feature decorrelation and re-normalization for color transfer, handcrafted filters for cartoon-like effect, markovian random field for modeling texture et al. We also discussed the limitation of these classical methods mainly comes from the low-level feature representation and all the higher-level model assumptions built upon it.

With such knowledge, we move on to the recent development of deep learning-based style transfer techniques. We first discuss using feature learned from deep neural networks to improve the classical parametric and non-parametric style transfer methods. For example, fit statistical distribution to deep features is a very effective way to model painterly texture; whitening and coloring deep features enables a closed-form solution for universal style transfer; Markovian Random Fields can be applied in deep feature maps to improve the results of non-parametric texture transfer.

Last but not least, we highlight the implication of generative adversarial networks in style transfer and conclude its advantage in modeling complex and photorealistic textures. We believe GANs’ unmatched ability to learning from unpaired data and avoiding handcrafting model representation/learning metric make it a very powerful tool for developing novel style transfer techniques.

1. Painted by the Dutch post-impressionist painter Vincent van Gogh, The Starry Night is one of the most recognized paintings in the history of Western culture. Painted in June 1889, it describes the view from the east-facing window of his asylum room at Saint-Rémy-de-Provence, just before sunrise, with the addition of an ideal village. MOMA New York: This mid-scale, oil-on-canvas painting is dominated by a moon- and star-filled night sky. It takes up three-quarters of the picture plane and appears turbulent, even agitated, with intensely swirling patterns that seem to roll across its surface like waves. It is pocked with bright orbs—including the crescent moon to the far right, and Venus, the morning star, to the left of center—surrounded by concentric circles of radiant white and yellow light. Beneath this expressive sky sits a hushed village of humble houses surrounding a church, whose steeple rises sharply above the undulating blue-black mountains in the background. A cypress tree sits at the foreground of this night scene. Flame-like, it reaches almost to the top edge of the canvas, serving as a visual link between land and sky. Considered symbolically, the cypress could be seen as a bridge between life, as represented by the earth, and death, as represented by the sky, commonly associated with heaven. Cypresses were also regarded as trees of the graveyard and mourning. The Starry Night is based on van Gogh’s direct observations as well as his imagination, memories, and emotions. The steeple of the church, for example, resembles those common in his native Holland, not in France. The whirling forms in the sky, on the other hand, match published astronomical observations of clouds of dust and gas known as nebulae. At once balanced and expressive, the composition is structured by his ordered placement of the cypress, steeple, and central nebulae, while his countless short brushstrokes and thickly applied paint set its surface in roiling motion. Image source: Wikipedia. ↩

2. No. 5, 1948 is a painting by Jackson Pollock, an American painter known for his contributions to the abstract expressionist movement. It was sold in May 2006 for $140 million, a new mark for highest ever price for a painting, not surpassed until April 2011. On inspection it was grey, brown, white and yellow paint drizzled in a way that many people still perceive as a “dense bird’s nest”. wikipedia: The painting was created on a 8’ x 4’ fibreboard. For the paint, Pollock chose to use liquid paints. More specifically, they were synthetic resin paints (gloss enamel) but are referred to as oil paints for classification of the work. On inspection it was grey, brown, white and yellow paint drizzled in a way that many people perceive as a “dense bird’s nest”. highbrow: all of Pollock’s drip period paintings were created by laying a piece of fiberboard on the floor to use as a canvas, giving the artist the greatest number of angles and range of motion to splash, smear, splatter, drip, fling, and pour his paints into an image. In No. 5, 1948 specifically, viewers can see Pollock’s use of black, white, grey, red, and yellow overlapping in layers that interweave and cover the entire surface area. The movement is constant, pooling in larger spots and exploding in multiple directions at once. Although the colors are simple, the directions and conscious way in which Pollock applied them creates an emotional flow through the lines. Recently, scholars have shown that Pollock’s angles and implied motions display mathematical precision. ↩

3. Deep Photo Style Transfer Proposed by Luan et al, the neural networks based method can transfer photorealistic style from one image to another. The main contribution is to constraint the transformation from the input to the output to be locally affine in colorspace, and to express this constraint as a custom fully differentiable energy term. The authors showed that this approach successfully suppresses distortion and yields satisfying photorealistic style transfers in a broad variety of scenarios, including transfer of the time of day, weather, season, and artistic edits. Formally, the authors build upon the Matting Laplacian of Levin et al. who have shown how to express a grayscale matte as locally affine combination of the input RGB channels. A least-squares penalty function can be minimized with a standard linear system represented by a matrix $M_{I}$ that only depends on the input image $I$. The locall affine regularizer is then defined as $\sum_{c=1}^{3}V_{c}[O]^TM_{I}V_{c}[O]$, where $V_{c}[O]$ is the vectorized version $(N\times1)$ of the output image $O$ in channel $c$. Using this term in a gradient-based solver requires computing its derivative w.r.t. the output image. Since $M_{I}$ is a symmetric matrix, we have: $\frac{dL_{m}}{dV_{c}[o]}=2M_{I}V_{c}[O]$. The optimization is futher augmented with semantic segmentation. Image source: Deep Photo Style Transfer, Luan et al. ↩

4. Everybody Dance Now Proposed by Chan et al, this technique is capable of “do as I do” motion transfer: given a source video of a person dancing it can transfer that performance to a novel (amateur) target after only a few minutes of the target subject performing standard moves. 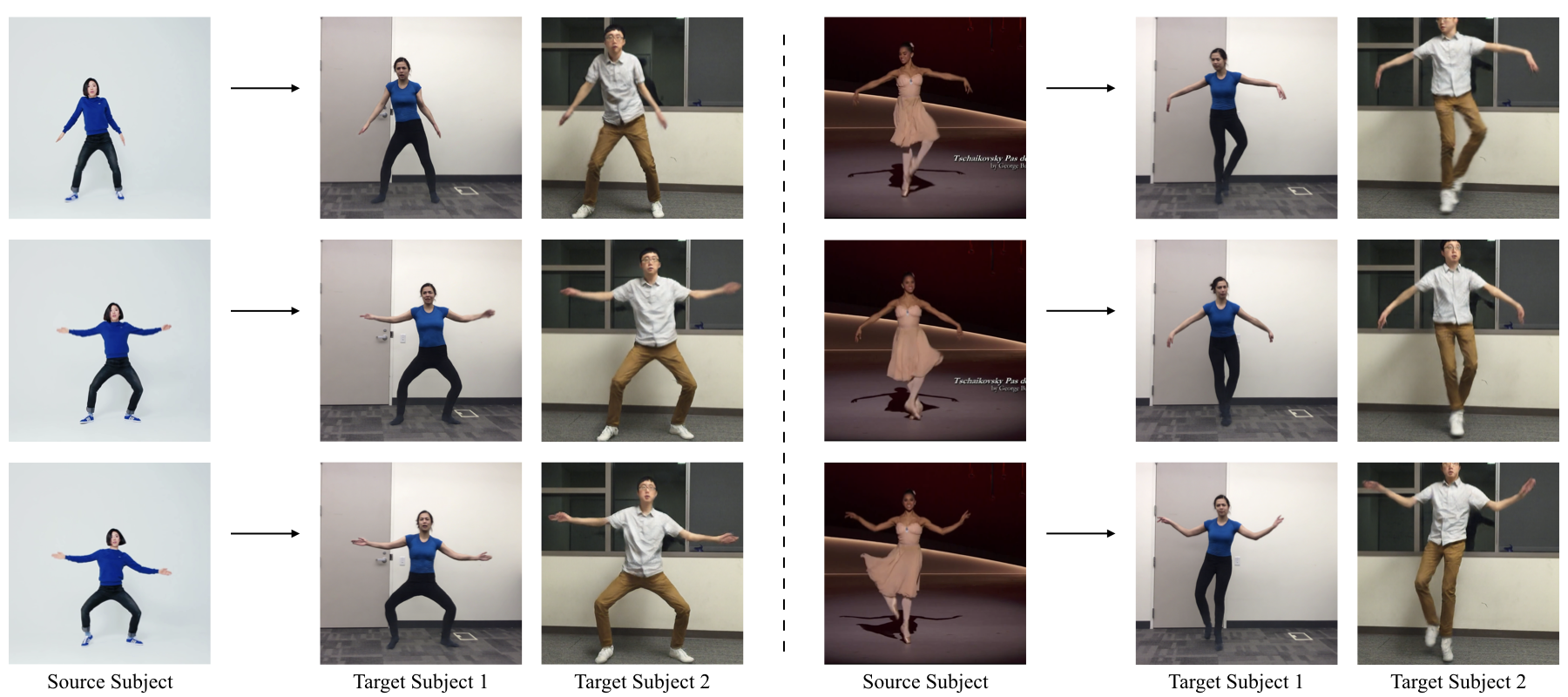The authors pose this problem as a per-frame image-to-image translation with spatio-temporal smoothing. Using pose detections as an intermediate representation between source and target, the technique learn a mapping from pose images to a target subject’s appearance. Below is the learning pipeline: 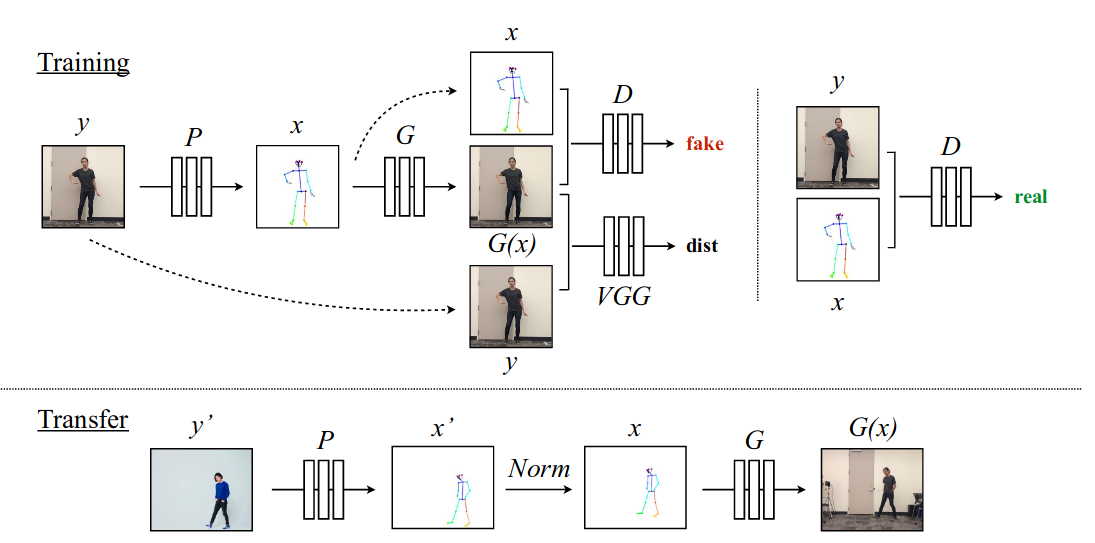Notice the VGG dist to measure the perceptual reconstruction loss. Temporal smoothing is achieved by synthesizing the current frame $G(X_t)$ conditioned on its corresponding pose stick figure $X_t$ and the previously synthesized frame $G(X_t−1)$ to obtain temporally smooth outputs. Discriminator $D$ then attempts differentiate the “real” temporally coherent sequence $(X_{t−1},X_t,Y_{t−1}, Y_t)$ from the “fake” sequence $(X_{t−1}, X_t, G(X_{t−1}), G(X_t))$. Image source: Everybody Dance Now, Chan et al. ↩

5. Image processing is the method of using algorithms to process digital images. It is a fundamental field for low level computer vision, and involves techniques such as sampling, filtering, transforming, compression et al. Below shows the result of Canny Edge Detection – a very important method for extracting edge information for many downstream vision tasks. Image source: wikipedia. ↩

6. Feature detection is the method of extracing useful features from images, including edges, corners/interest points, blobs/interest regions etc. Below is an example of Harris corner detector. It uses the second-moment matrix to summerize the predominant directions of the gradient in a specific pixel’s neighbourhood. The eigenvalues of the matrix are used to calculate the corner response. Non-maximum supperssion is used to pick up the most predominant pixel as a corner from a local neighborhood. Image source: wikipedia. ↩

7. Image segmentation is the process of partitioning a digital image into multiple segments (sets of pixels, also known as super-pixels). The goal of segmentation is to simplify and/or change the representation of an image into something that is more meaningful and easier to analyze. The Contour Detection and Image Segmentation Resources from Computer Vision Group at UC Berkeley is a classical dataset for benchmarking image segmentation technique. More recently the Microsoft Common Objects in Context (MSCOCO) datas has become the de-facto resource for large-scale object detection, segmentation and captioning. Image source: MSCOCO website. ↩

8. Texture refers to every digital image composed of repeated elements. The image below shows different textures along a spectrum going from regular to stochastic. Texture analysis and synthesis study the problem of extracting useful information from an example texture, and creates new textured images of similar characteristics. Image source: wikipedia. ↩

9. A Parametric Texture Model Based on Joint Statistics of Complex Wavelet Coefficients present a universal statistical model for texture images in the context of an overcomplete complex wavelet transform. The model is parameterized by a set of statistics computed on pairs of coefficients corresponding to basis functions at adjacent spatial locations, orientations, and scales. Below are examples of texture synthesized with this method. The top row are the reference texture (real images), the bottom row are the synthesized images (fake images) that look like the reference. Image source: A Parametric Texture Model Based on Joint Statistics of Complex Wavelet Coefficients, J Portilla et al. ↩

10. Texture Synthesis by Non-parametric sampling is a landmark research of A. Efros et al. The method grows a new image outward from an initial seed, one pixel at a time. A Markov random field model is assumed, and the conditional distribution of a pixel given all its neighbors synthesized so far is estimated by querying the sample image and finding all similar neighborhoods. The degree of randomness is controlled by the size of neighborhood window. The method preservs as much local structure as possible and produces good results for a wide variety of synthetic and real-world textures. The top left region in the image below is the example from where the rest of the image is syntheized. Image source: Texture Synthesis by Non-parametric sampling, A. Efros et al. ↩ ↩²

11. Texture Optimiztion for Example based Texture Synthesis present a Markov Random Field (MRF)-based similarity metric for measuring the quality of synthesized texture with respect to a given input sample. It allows us to formulate the synthesis problem as minimization of an energy function, which is optimized using an Expectation Maximization (EM)-like algorithm. The image below shows the minization and the process that the output image envolves to a visually plausible texture. 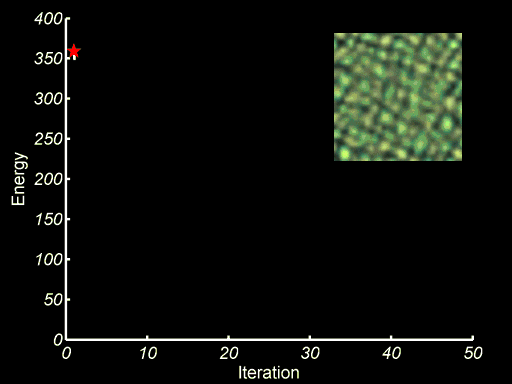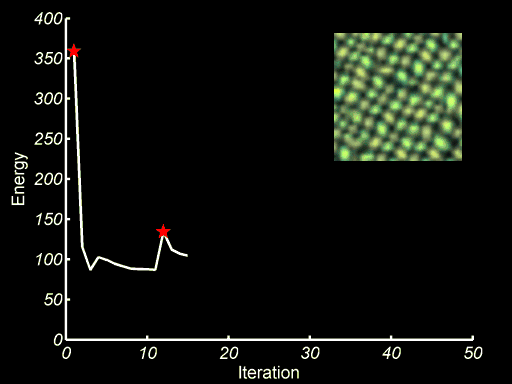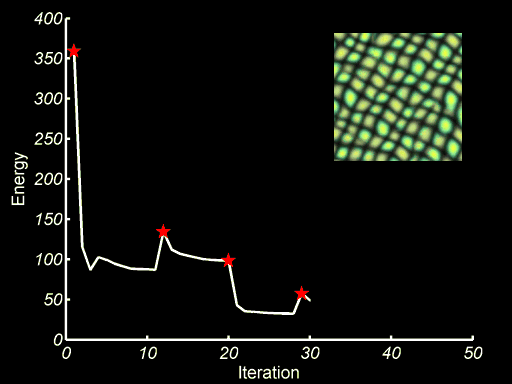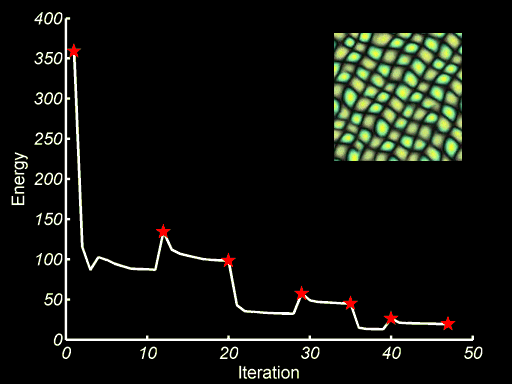Image source: Texture Optimiztion for Example based Texture Synthesis, V Kwatra et al. ↩

12. Autoencoder is a neural network that learns to reconstruct its input as its output. It is constituted by two main parts: an encoder that maps the input into a latent code, and a decoder that maps the latent code to a reconstruction of the original input. By making the latent code much smaller than the input image, the autoencoder learns to produce a compact encoding of the image. For this reason, Autoencoder is widely used as a unsupervised method for extracting useful image representation. 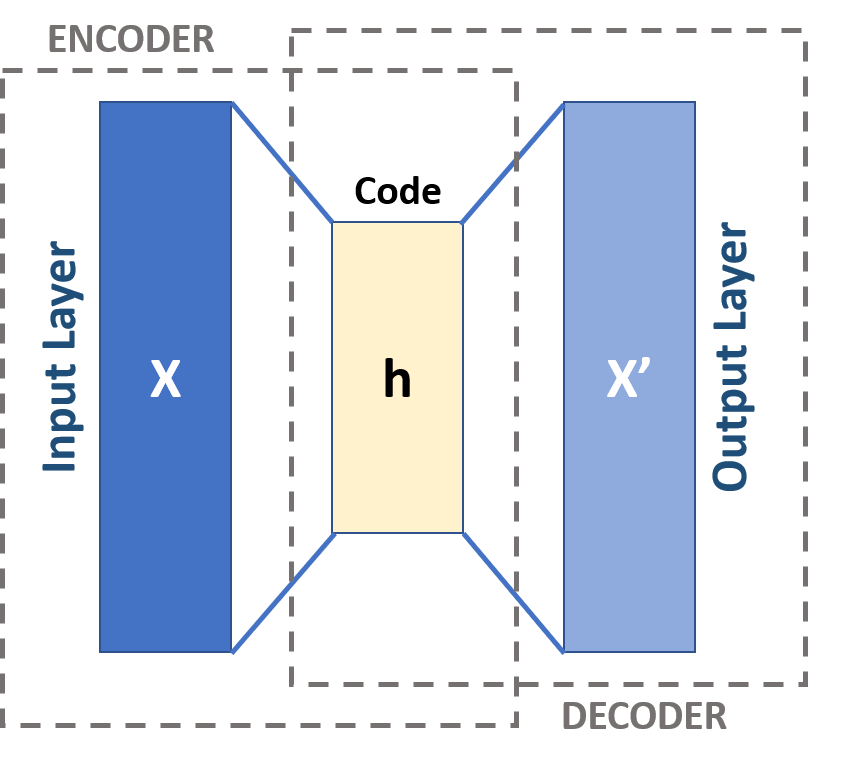. Image source: Wikipedia. ↩

13. Generative models are statistical models that, given an observable variable X and a target variable Y, model the joint probability distribution on X × Y. This is different from the discriminative models (classifiers etc.) which model the conditional probability of the target Y (for example, class label), given an observation of X (for example, image). ↩

14. Generative adversarial networks (GANs) is a class of machine learning systems invented by I. Goodfellow et al. Two neural networks contest with each other in a game (in the sense of game theory, often but not always in the form of a zero-sum game), so the discriminator learns to classify the fake (generated) samples from the real samples (from training set), whereas the generator learns to produce samples that can fool the discriminator. This eventually let the generator learns to generate new data with the same statistics as the training set. For example, a GAN trained on photographs can generate new photographs that look at least superficially authentic to human observers, having many realistic characteristics. The image below shows the training process of GANs: 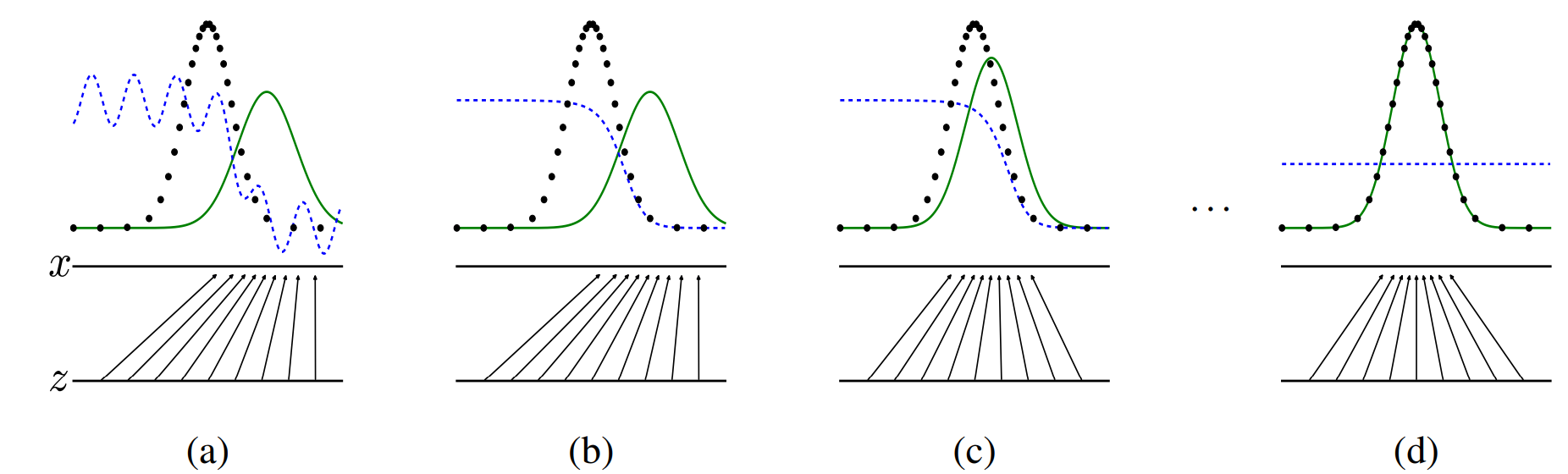Generative adversarial nets are trained by simultaneously updating the discriminative distribution ($D$, blue, dashed line) so that it discriminates between samples from the data generating distribution (black, dotted line) $p_x$ from those of the generative distribution $p_g(G)$ (green, solid line). The lower horizontal line is the domain from which $z$ is sampled, in this case uniformly. The horizontal line above is part of the domain of $x$. The upward arrows show how the mapping $x = G(z)$ imposes the non-uniform distribution $p_g$ on transformed samples. $G$ contracts in regions of high density and expands in regions of low desnsity of $p_g$. (a) Consider an adversarial pair near convergence: $p_g$ is similar to $p_{data}$ and $D$ is a partially accurate classifier. (b) In the inner loop of the algorithm $D$ is trained to discriminate samples from data, converging to $D^{\star}(x)=\frac{p_{data}(x)}{p_{data}(x) + p_{y}(x)}$. (c) After an update to $G$, gradient of $D$ has guided $G(z)$ to flow to regions that are more likely to be classified as data. (d) After serveral steps of training, if $G$ and $D$ have enough capacity, they will reach a point at which both cannot improve because $p_g = p_{data}$. The discriminator is unable to differentiate between the two distributions, i.e. $D(x) = \frac{1}{2}$. Image Source: Generative Adversarial Networks, I Goodfellow et al. ↩ ↩²

15. Hairy brushes. S. Strassmann, Siggraph 1986. Paint brushes are modeled as a collection of bristles which evolve over the course of the stroke, leaving a realistic image of a sumi brush stroke. Image source: Hairy brushes, S. Strassmann. ↩

16. Fast paint texture. A. Hertzmann, NPAR 2002. A technique for simulating the physical appearance of paint strokes under lighting. This technique is easy to-implement and relatively fast, yet produces realistic results. The system processes a painting composed of a list of brush strokes. A height map is assigned to each stroke, and a height field for the painting is produced by rendering the brush strokes textured with the height maps. The final painting is rendered by bump-mapping the painting’s colors with the height map. The entire process takes only a few seconds on current hardware. Image Source: Fast Paint Texture, A. Hertzmann. ↩ ↩²

17. Computer-Generated Watercolor. C. Curtis et al, Siggraph 97. Watercolor model is based on an ordered set of translucent glazes, which are created independently using a shallow-water fluid simulation. The method used a Kubelka-Munk compositing model for simulating the optical effect of the superimposed glazes. Image source: Computer-Generated Watercolor, C. Curtis et al. ↩ ↩²

18. Painterly Rendering with Curved Brush Strokes of Multiple Sizes is a method for creating an image with a handpainted appearance from a photograph, and an approach to designing styles of illustration. The method paints an image with a series of spline brush strokes. Brush strokes are chosen to match colors in a source image. A painting is built up in a series of layers, starting with a rough sketch drawn with a large brush. The sketch is painted over with progressively smaller brushes, but only in areas where the sketch differs from the blurred source image. Thus, visual emphasis in the painting corresponds roughly to the spatial energy present in the source image. The image below shows (a) A source image. (b) The first layer of a painting, after painting with a circular brush of radius 8. (c) The image after painting with a brush of radius 4. (d) The final image, after painting with a brush of size 2. Note that brush strokes from earlier layers are still visible in the painting. Image Source: Painterly Rendering with Curved Brush Strokes of Multiple Sizes, A Hertzmann. ↩ ↩²

19. Processing images and video for an impressionist effect A technique that transforms ordinary video segments into animations that have a hand-painted look. The method is the first to exploit temporal coherence in video clips to design an automatic filter with a hand-drawn animation quality, in this case, one that produces an Impressionist effect. The image below shows the original image (left) and the processed image using no brush stroke clipping and a constant base stroke orientation of 45°. Image Source: Processing images and video for an impressionist effect, P Litwinowicz et al. ↩

20. Interactive pen-and-ink illustration. M. Salisbury. Siggraph 2002. This technique presented an interactive system for creating pen-and-ink illustrations. The system uses stroke textures—collections of strokes arranged in different patterns—to generate texture and tone. The user “paints” with a desired stroke texture to achieve a desired tone, and the computer draws all of the individual strokes. The image below using a grey scale image for reference. Left to right: Original grey scale image; extracted edges; curved hatching across the gradient. Image Source: Interactive pen-and-ink illustration, M. Salisbury et al. ↩ ↩²

21. Paint by numbers: abstract image representations This technique showed that it is possible to create abstract images using an ordered collection of brush strokes. These abstract images filter and refine visual information before it is presented to the viewer. By controlling the color, shape, size, and orientation of individual brush strokes, impressionistic paintings of computer generated or photographic images can easily be created. Image Source: Paint by numbers: abstract image representations, P Haeberli et al. ↩

22. Color Transfer Between Images, E. Reinhard et al., 2001. proposed an elegant approach to transfer the color of one image to another image. The below images shows the result of transfer the color scheme of a Van Gogh’s painting to a photo. Formally, let $[l_{s}, \alpha_{s}, \beta_{s}]$ and $[\sigma_{s}^{l}, \sigma_{s}^{\alpha}, \sigma_{s}^{\beta}]$ denote the mean and standard deviation of the source image’s three channels (the photo), and $[l_{t}, \alpha_{t}, \beta_{t}]$ and $[\sigma_{t}^{l}, \sigma_{t}^{\alpha}, \sigma_{t}^{\beta}]$ denote the mean and standard deviation of the target image (the painting). The transfer is applied as such: $l'=(l - l_{s})\frac{\sigma_{t}^l}{\sigma_{s}^l} + l_{t}, \ \ \ \alpha'=(\alpha - \alpha_{s})\frac{\sigma_{t}^\alpha}{\sigma_{s}^\alpha} + \alpha_{t}, \ \ \ \beta'=(\beta - \beta_{s})\frac{\sigma_{t}^\beta}{\sigma_{s}^\beta} + \beta_{t}$ Image source: Color Transfer Between Images, E. Reinhard et al. ↩ ↩² ↩³ ↩⁴

23. Image Style Transfer Using Convolutional Neural Networksfrom L. Gatys et al. CVPR 2016 is a landmark work of style transfer in the deep learning area. The image below shows the result of transfer the style of an oil painting to a photo. Formally, the style is modeled by the Gram Matrix of the target (style) image’s feature activations from a particular layer: Gram matrix $G^l \in R^{N_l \times N_l}$, where $G_{i,j}^l$ is the inner product between the vectorised feature channel $i$ and $j$ in layer $l$: $G_{i,j}^{l}=\sum_{k}F_{ik}^lF_{jk}^l$. Let the gram matrix of the same layer of the source (content) image be $A^l$, then the style loss is defined as $E^l=\frac{1}{4N_{l}^2M_{l}^2}\sum_{i,j}(G_{ij}^l - A_{ij}^l)^2$. In practice, Gram metrics from multiple layers are used to capture the style at different scales, so the final total style loss is defined as $L_{style}(\hat{a}, \hat{x} = \sum_{l=0}^{L}w_lE_l$ where $w$ are the weights for individual layers. Image source: Image Style Transfer Using Convolutional Neural Networks, L. Gatys et al. ↩ ↩² ↩³ ↩⁴ ↩⁵ ↩⁶

24. Universal Style Transfer via Feature Transforms. Y. Li et al. Formally, the whitening transformation and coloring transformations that map content feature $f_c$ to stylized feature $f_{cs}$ are defined as the follwing: $\hat{f}_{c} = E_{c}D_{c}^{-\frac{1}{2}}E_{c}^{T}f_{c}, \ \ \ \hat{f_{cs}} = E{s}D_{s}^{\frac{1}{2}}E_{s}^{T}\hat{f_{c}}$ The first equation is the whitening operation: $D_{c}$ is a diagonal matrix with the eigenvalues of the covariance matrix $f_{c}f_{c}^{T} \in\Re^{C \times C}$, and $E_{c}$ is the corresponding orthogonal matrix of eigenvectors, satisfying $f_{c}f_{c}^{T} = E_{c}D_{c}E_{c}^{T}$. The whitened feature map satisfies $\hat{f_{C}}\hat{f_{C}^{T}} = I$. The second equation is the coloring operation: where $D_{s}$ is a diagonal matrix with the eigenvalues of the covariance matix $f_{s}f_{s}^{T} \in \Re^{C \times C}$, and $E_{s}$ is the corresponding orthogonal matrix of eigenvalues. The coloring operation satisfies $\hat{f_{cs}}\hat{f_{cs}}^{T} = f_{s}f_{s}^{T}$. Finally the colored feature map $\hat{f_{cs}}$ is re-centerred with the mean of the style features: $\hat{f_{cs}} = \hat{f_{cs}} + m_{s}$. Overall, the fact that the coloring operation satisfies $\hat{f_{cs}}\hat{f_{cs}}^{T} = f_{s}f_{s}^{T}$ means the distribution of transferred features match the distribution of target style features from the perspective of how whitened features correlated. ↩ ↩² ↩³

25. State of the ‘Art’: A Taxonomy of Artistic Stylization Techniques for Images and Video. J Kyprianidis et al. TVCG 2013. ↩

26. Real-time video abstraction. H. Winnemöller et al. Siggraph 2006. This technique present an automatic, real-time video and image abstraction framework that abstracts imagery by modifying the contrast of visually important features, namely luminance and color opponency. The method reduces contrast in low-contrast regions using an approximation to anisotropic diffusion, and artificially increase contrast in higher contrast regions with difference-of-Gaussian edges. The abstraction step is extensible and allows for artistic or data-driven control. 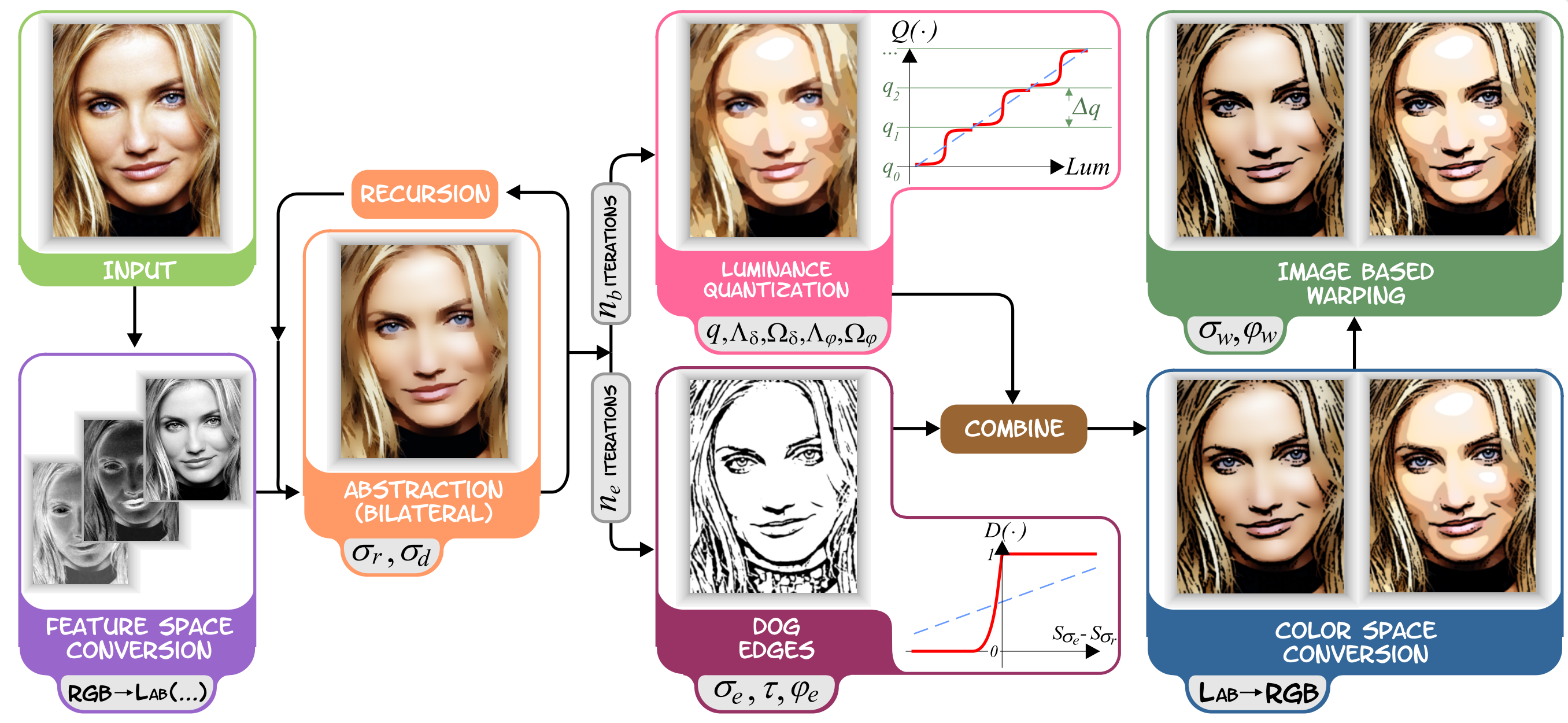Image Source: Real-time video abstraction, H. Winnemöller et al. ↩

27. Mean shift: A robust approach toward feature space analysis A general non-parametric technique is proposed for the analysis of a complex multimodal feature space and to delineate arbitrarily shaped clusters in it. The basic computational module of the technique is an old pattern recognition procedure: the mean shift. For discrete data, the method prove the convergence of a recursive mean shift procedure to the nearest stationary point of the underlying density function and, thus, its utility in detecting the modes of the density. Below shows the application of the algorithm in image segmentation Image Source: Mean shift: A robust approach toward feature space analysis, D Comaniciu et al. ↩

28. Stylization and Abstraction of Photographs The authors proposed a computational approach to stylizing and abstracting photographs that explicitly responds to this design goal. The system transforms images into a line-drawing style using bold edges and large regions of constant color. To do this, it represents images as a hierarchical structure of parts and boundaries computed using state-of-the-art computer vision. The system identifies the meaningful elements of this structure using a model of human perception and a record of a user’s eye movements in looking at the photo; the system renders a new image using transformations that preserve and highlight these visual elements. Image Source: Stylization and Abstraction of Photographs, D DeCarlo et al. ↩

29. Video Tooning A system is proposed for transforming an input video into a highly abstracted, spatio-temporally coherent cartoon animation with a range of styles. To achieve this, the system treats video as a space-time volume of image data. An anisotropic kernel mean shift technique is developed to segment the video data into contiguous volumes. These provide a simple cartoon style in themselves, but more importantly provide the capability to semi-automatically rotoscope semantically meaningful regions. The image below compares radially symmetric kernel mean shift (left) and anisotropic kernel mean shift(right) on a spatio-temporal slice of the monkey bars sequence. The straighter edges in vertical (temporal) dimension lead to improved temporal coherence. Image Source: Video Tooning, J Wang et al. ↩

30. Stroke surfaces: Temporally coherent non-photorealistic animations from video The below image is A visualization of the Stroke Surfaces generated from a video sequence, which, when intersected by the a time plane, generate the region boundaries of a temporally coherent segmentation. The boundary of single video object, for example, the sheep’s body, may be described by multiple Stroke Surfaces. The image below compares radially symmetric kernel mean shift (left) and anisotropic kernel mean shift(right) on a spatio-temporal slice of the monkey bars sequence. The straighter edges in vertical (temporal) dimension lead to improved temporal coherence. 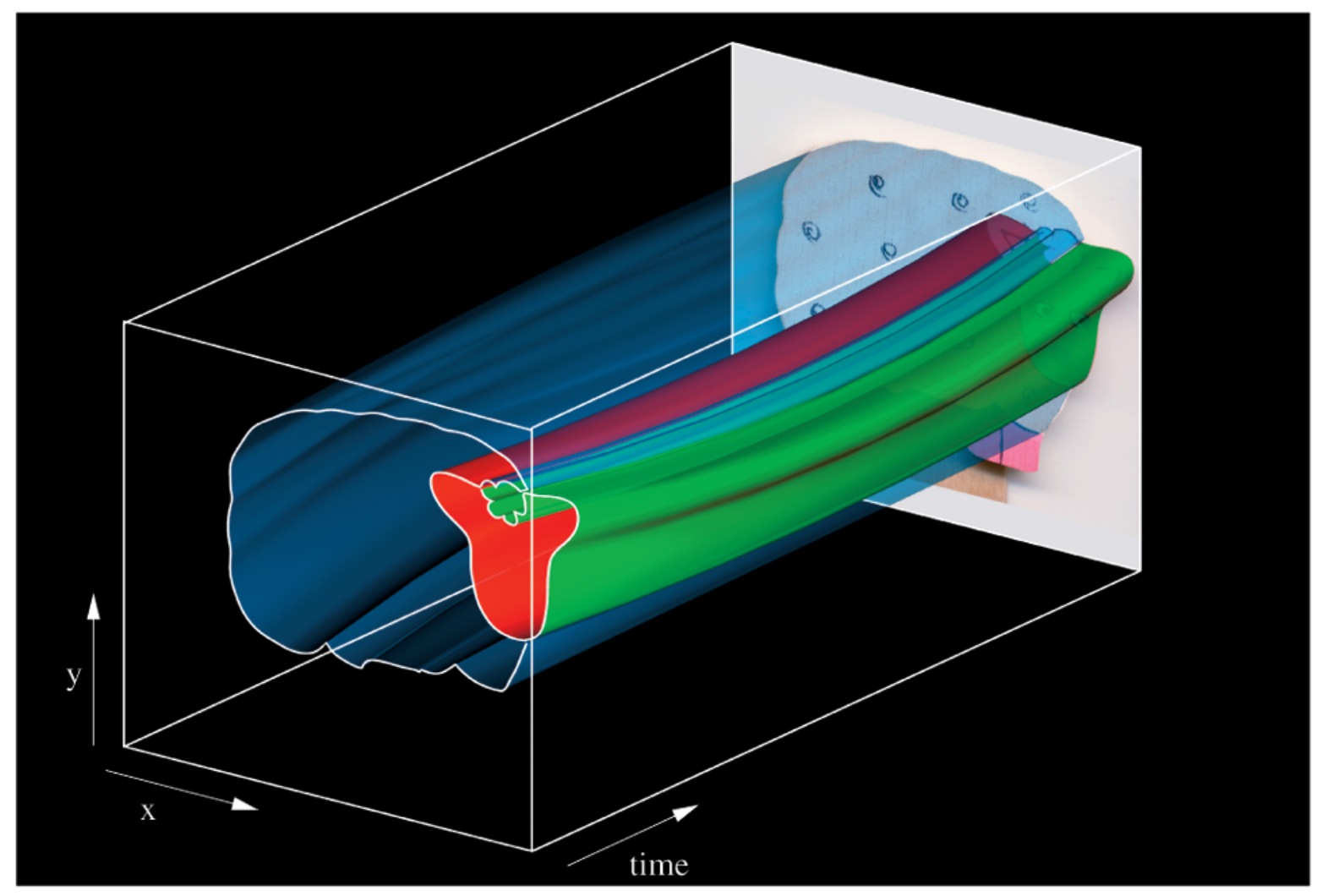Image Source: Stroke surfaces: Temporally coherent non-photorealistic animations from video, JP Collomosse et al. ↩

31. Arty Shapes The technique shows that shape simplification is a tool useful in Non-Photorealistic rendering from photographs, because it permits a level of abstraction otherwise unreachable. A variety of simple shapes (e.g. circles, triangles, squares, superellipses and so on) are optimally fitted to each region within a segmented photograph. The system automatically chooses the shape that best represents the region; the choice is made via a supervised classifier so the “best shape” depends on the subjectivity of a user. Image Source: Arty Shapes, YZ Song et al. ↩

32. Image Analogies. Aaron Hertzmann et al. The technique describes a new framework for processing images by example, called “image analogies.” The framework involves two stages: a design phase, in which a pair of images, with one image purported to be a “filtered” version of the other, is presented as “training data”; and an application phase, in which the learned filter is applied to some new target image in order to create an “analogous” filtered result. Image Source: Image Analogies, A Hertzmann et al. ↩ ↩²

33. Paint By Relaxation The technique use relaxation to produce painted imagery from images and video. An energy function is first specified; it then searches for a painting with minimal energy. The appeal of this strategy is that, ideally, we need only specify what we want, not how to directly compute it. Because the energy function is very difficult to optimize, the technique use a relaxation algorithm combined with search heuristics. The image below greedy paintly rendering method of with 1 and 2, layers, respectively. The algorithm has difficulty capturing detail below the stroke size. Bottom: Paint by relaxation, with 1 and 2 layers. Strokes are precisely aligned to image features, especially near sharp contours, such as the lower-right corner of the jacket. Image Source: Paint By Relaxation, A Hertzmann et al. ↩

34. Image Quilting. A. Efros et al. The technique first uses quilting as a fast and very simple texture synthesis algorithm which produces surprisingly good results for a wide range of textures. Second, the technique extends the algorithm to perform texture transfer – rendering an object with a texture taken from a different object. More generally, the technique demonstrate how an image can be re-rendered in the style of a different image. The method works directly on the images and does not require 3D information. The image below highlights the pixels and image patches that excite the neuron at one layer of a deep neural network. Image Source: Image Quilting, A. Efros et al. ↩ ↩²

35. Min-cut/Max flow theorem is an important technique for exacting or approximating energy minimization in low-level computer vision. In particular, image segmentation can be considerred as a labeling problem that minimizes the below energy: $E(f) = \sum_{p \in P}D_{p}(i_p, f_p) + \sum_{p,q\in N}V_{p,q}(f_p,f_q)$ The first term is known as the datat term, which measures the cost of labeling a single pixel $p$ with a class id $f_p$. The second term is known as the smooth term. It penalizes the inconsistent labels $f_p$ and $f_q$ between two adjacent pixels. The combination of these two terms make the segmentation accuracy and smooth. The seminal work of Boykov et al. Fast Approximate Energy Minimization via Graph Cuts proposed two algorithms that use graph cuts to compute a local minimum even when very large moves are allowed. The first move is $\alpha$-$\beta$-swap: for a pair of labels: $\alpha$ and $beta$, this move exchanges the labels between an arbitrary set of pixels labeled $\alpha$ and another arbitrary set labeled $\beta$. The $\alpha$-$\beta$-swap algorithm generates a labeling such that there is no swapmove that decreases the energy. The second method is $\alpha$-expansion: for a label $\alpha$, this move assigns an arbitrary set of pixels the label. This algorithm requires the smoothness term to be a metric, and generates a labeling such that there is noexpansion move that decreases the energy. ↩

36. Visualizing and Understanding Convolutional Networks. M. Zeiler et al. To examine a convnet, a deconvnet is attached to each of its layers, providing a continuous path back to image pixels. To start, an input image is presented to the convnet and features computed throughout the layers. To examine a given convnet activation, the method sets all other activations in the layer to zero and pass the feature maps as input to the attached deconvnet layer. Then the method successively (i) unpool, (ii) rectify and (iii) filter to reconstruct the activity in the layer beneath that gave rise to the chosen activation. This is then repeated until input pixel space is reached. In the below image shows the image patches that excite particular neurons in one layer of a networks (right). To highlight the pixels that contribute the most to the activation, the method backpropagates the activation to the input patch (left). Image Source: Visualizing and Understanding Convolutional Networks, M. Zeiler et al. ↩

37. Understanding Deep Image Representations by Inverting Them. A. Mahendran et al. 2014. The authors conduct a direct analysis of the visual information contained in representations by asking the following question: given an encoding of an image, to which extent is it possible to reconstruct the image itself? To answer this question the authors contribute a general framework to invert representations. The image below shows the reconstruction using feature maps at different layers of a deep neural networks. Image Source: Understanding Deep Image Representations by Inverting Them, A. Mahendran et al. ↩ ↩² ↩³

38. Synthesizing the preferred inputs for neurons inneural networks via deep generator networks. A. Nguyen et al. NIPS 2016. The authors dramatically improve the qualitative state of the art of activation maximization by harnessing a powerful, learned prior: a deep generator network (DGN). Instead of updating pixel values, the method backpropogate the gradient further to a lantent encoding of the output image. After the encoding is then updated by the gradient, the deep generator network is used to decode the updated encoding to the output image. In this way, the output image is always comfront to the image priors in the deep generator network. The image below shows some of the visualizations. Image Source: Synthesizing the preferred inputs for neurons inneural networks via deep generator networks, A. Nguyen et al. ↩

39. The Building Blocks of Interpretability. C Olah. Distill 2018. The method treats existing interpretability methods as fundamental and composable building blocks for rich user interfaces. The authors find that these disparate techniques now come together in a unified grammar, fulfilling complementary roles in the resulting interfaces. Moreover, this grammar allows us to systematically explore the space of interpretability interfaces, enabling us to evaluate whether they meet particular goals. The image below pair every neuron activation with a visualization of that neuron and sort them by the magnitude of the activation. This marriage of activations and feature visualization changes our relationship with the underlying mathematical object. Image source: https://distill.pub/2018/building-blocks/ ↩

40. Inceptionism: Going Deeper into Neural Networks. A. Mordvintsev. Google AI blo 2015. By choosing higher-level layers, which identify more sophisticated features in images, complex features or even whole objects tend to emerge. Just start with an existing image and give it to our neural net. We ask the network: “Whatever you see there, I want more of it!” This creates a feedback loop: if a cloud looks a little bit like a bird, the network will make it look more like a bird. This in turn will make the network recognize the bird even more strongly on the next pass and so forth, until a highly detailed bird appears, seemingly out of nowhere. The image below shows some examples of hallucinated images. Image Source: Inceptionism: Going Deeper into Neural Networks, A Mordvintsev et al. ↩

41. Demystifying neural style transfer The authors theoretically show that matching the Gram matrices of feature maps is equivalent to minimize the Maximum Mean Discrepancy (MMD) with the second order polynomial kernel. The authors argue that the essence of neural style transfer is to match the feature distributions between the style images and the generated images. Experiments with several other distribution alignment methods showed appealing results. The image below shows style reconstructions of different methods in five layers, respectively. Each row corresponds to one method and the reconstruction results are obtained by only using the style loss. Because there is no content loss, the reconstruction in essence does free-form texture sythesis. . Image Source: Demystifying neural style transfer, Y Li et al. ↩

42. Limited-memory BFGS. Limited-memory BFGS (L-BFGS or LM-BFGS) is an optimization algorithm in the family of quasi-Newton methods that approximates the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm using a limited amount of computer memory. It is a popular algorithm for parameter estimation in machine learning. The basic idea is to use the inverse of the Hessian Matrix to approxite the local energy landscape as a parabolic surface, and update the model parameter direct to use the minima of the surface. ↩

43. Style Decomposition for Improved Neural Style Transfer ↩

44. Improved Style Transfer by Respecting Inter-layer Correlations. The authors proposed the cross-layer, rather than within-layer, gram matrices, to improve visual quality in style transfer. Formally, consider layer $l$ and $m$, both style layers with decreasing spatial resolution. Write $\uparrow f^{m}$ for an upsampling of $f^{m}$ to $H^{l}\times W^{l}\times K^{l}$, and $G^{l,m}_{ij}(I)=\sum[f^{l}_{i,p}(I)][\uparrow f^{m}_{j,p}(I)]^T$ is the cross channel gram matrix. ↩

45. Perceptual Losses for Real-Time Style Transfer and Super-Resolution The system overview: the authors train an image transformation network to transform input images into output images. The method uses a loss network pretrained for image classification to define perceptual loss functions that measure perceptual differences in content and style between images. The loss network remains fixed during the training process. 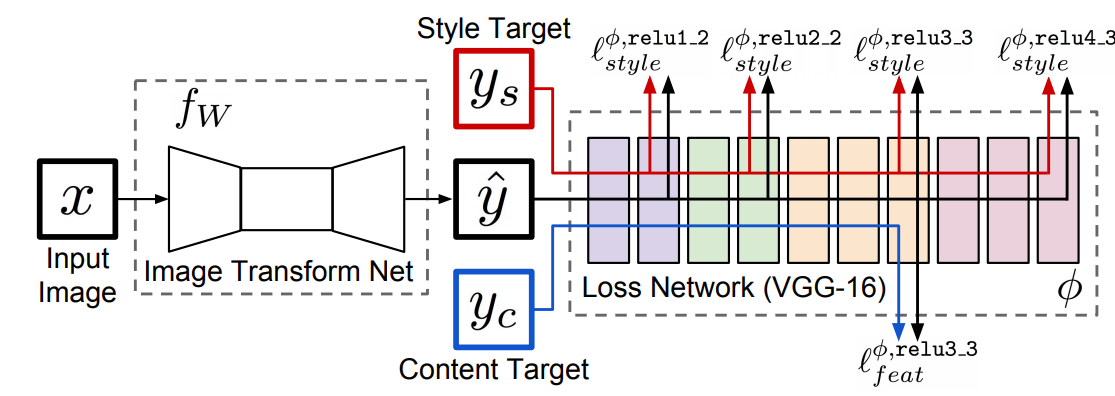Image Source: Perceptual Losses for Real-Time Style Transfer and Super-Resolution, J Johnson et al. ↩ ↩²

46. Texture Networks: Feed-forward Synthesis of Textures and Stylized Images. The system overview: a generator network (left) is traned using a powerful loss based on the correlation statistics inside a fixed pre-trained descriptor network (right). Of the two networks, only the generator is updated and later used for texture or image synthesis 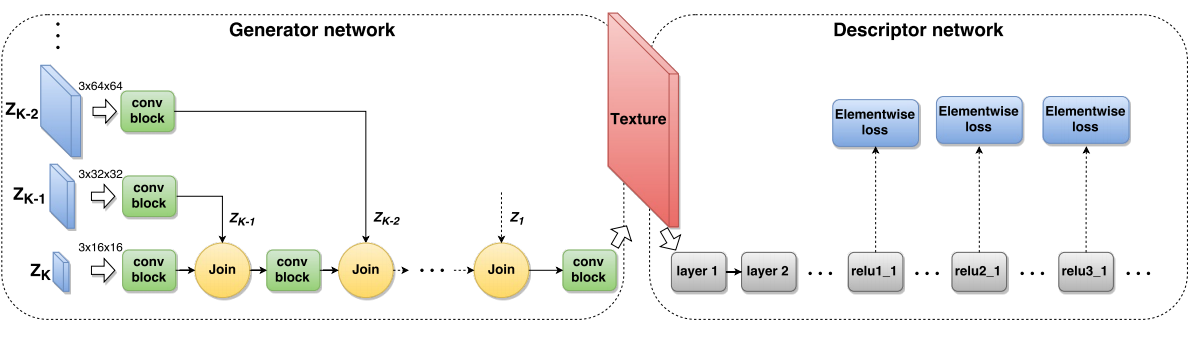Image Source: Texture Networks: Feed-forward Synthesis of Textures and Stylized Image, D Ulyanov et al. ↩ ↩²

47. Instance Normalization: The Missing Ingredient for Fast Stylization. The authors show how a small change in the stylization architecture results in a significant qualitative improvement in the generated images. The change is limited to swapping batch normalization with instance normalization, and to apply the latter both at training and testing times. The image below shows the improvement of instance normalization (right) over previous method (left, middle). Image Source: Instance Normalization: The Missing Ingredient for Fast Stylization, D Ulyanov et al. ↩

48. Real-Time Neural Style Transfer for Videos The feed-forward network is trained by enforcing the outputs of consecutive frames to be both well stylized and temporally consistent. Specifically, the difference between two consecutive stylized frames is penalized during training, whereas the first stylized frame is warpped by a pre-computed optical flow. This allows the method to produce less flickers. The image below shows the training pipeline, where the difference between two outputs $\hat{x}^{t}$ and $\hat{x}^{t-1}$ are used as the temporal loss to update the loss of individual frames, then the network parameters. 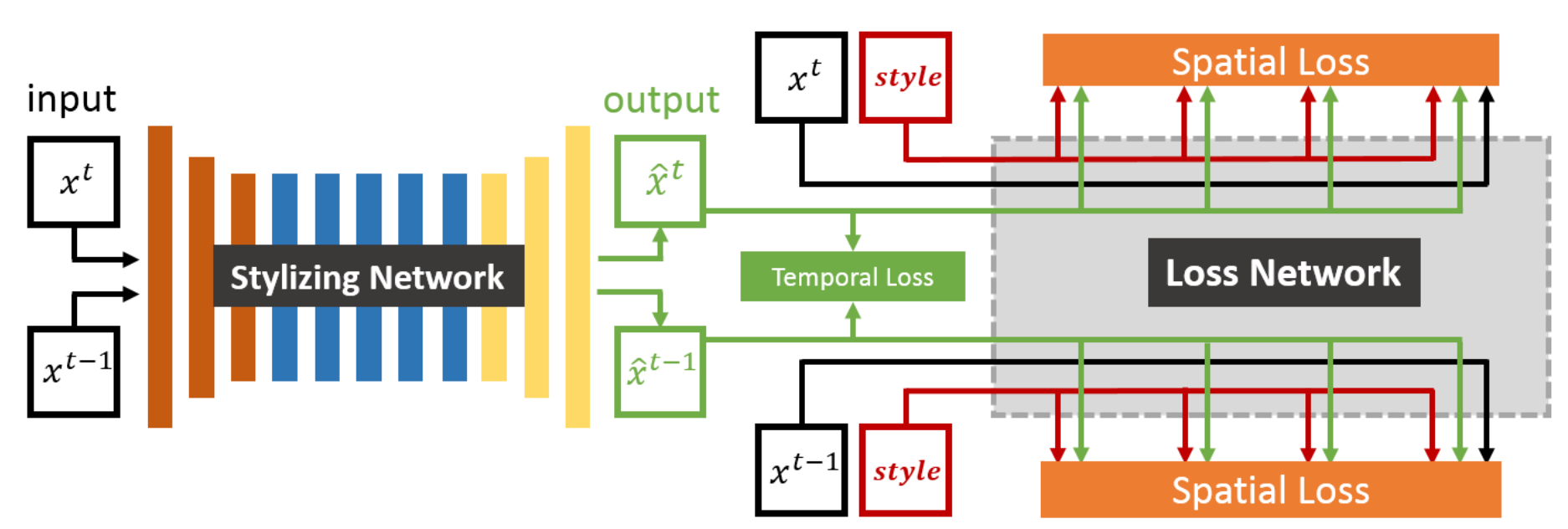Image Source: Real-Time Neural Style Transfer for Videos , H Huang et al. ↩

49. Characterizing and Improving Stability in Neural Style Transfer show that the trace of the Gram matrix representing style is inversely related to the stability of the method. The authors then proposed a recurrent convolutional network for real-time video style transfer which incorporates a temporal consistency loss and overcomes the instability of prior methods. ↩

50. Coherent Online Video Style Transfer The method incorporates short-term coherence, and propagates short-term coherence to long-term, which ensures the consistency over larger period of time. ↩

51. Arbitrary Style Transfer in Real-time with Adaptive Instance Normalization The authors present a simple yet effective approach that for the first time enables arbitrary style transfer in real-time. At the heart of our method is a novel adaptive instance normalization (AdaIN) layer that aligns the mean and variance of the content features with those of the style features. The below image shows the overview of the pipeline: the first few layers of a fixed VGG-19 network is used to encode the content and style images. An AdaIN layer is used to perform style transfer in the feature space. A decoder is learned to invert the AdaIN output to the image spaces. 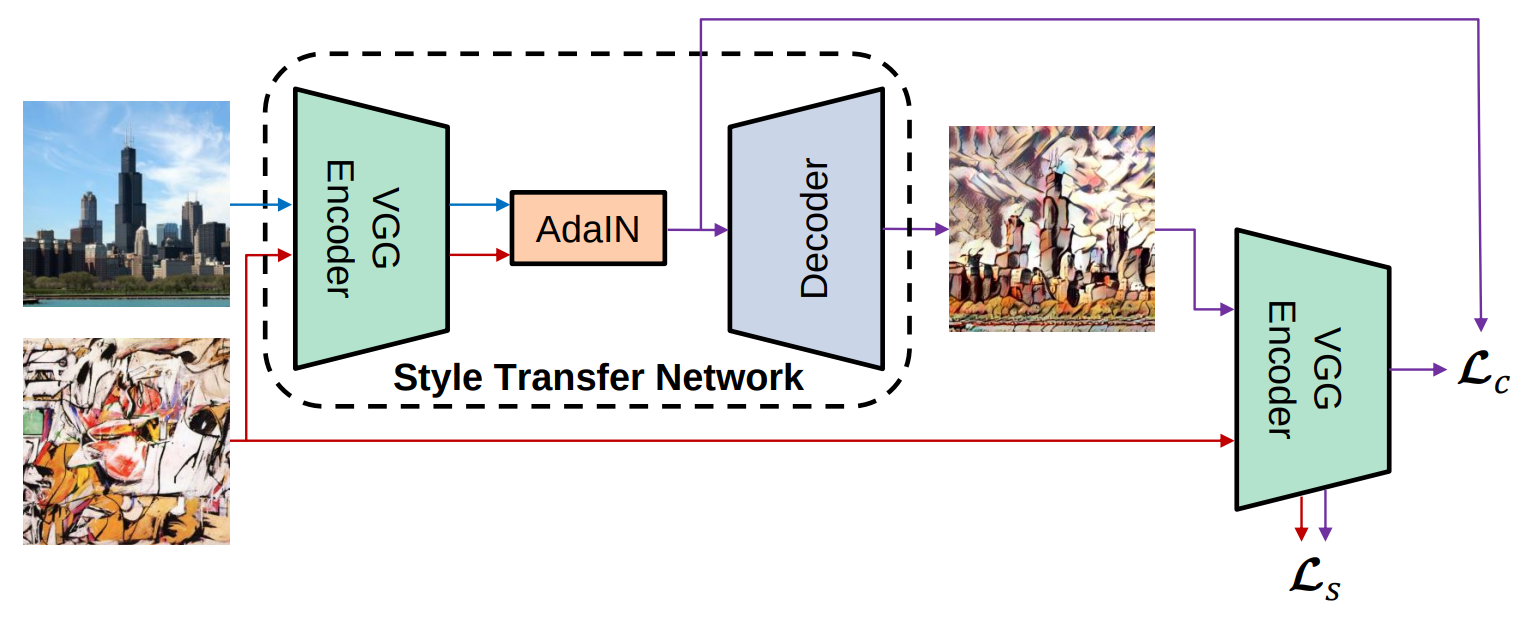Image Source: Arbitrary Style Transfer in Real-time with Adaptive Instance Normalization, X Huang et al. ↩

52. A Learned Representation For Artistic Style The authors investigate the construction of a single, scalable deep network that can parsimoniously capture the artistic style of a diversity of paintings. The method demonstrates that such a network generalizes across a diversity of artistic styles by reducing a painting to a point in an embedding space. Importantly, this model permits a user to explore new painting styles by arbitrarily combining the styles learned from individual paintings. ↩

53. StyleBank: An Explicit Representation for Neural Image Style Transfer StyleBank, which is composed of multiple convolution filter banks and each filter bank explicitly represents one style, for neural image style transfer. To transfer an image to a specific style, the corresponding filter bank is operated on top of the intermediate feature embedding produced by a single auto-encoder. The StyleBank and the auto-encoder are jointly learnt, where the learning is conducted in such a way that the auto-encoder does not encode any style information thanks to the flexibility introduced by the explicit filter bank representation. It also enables us to conduct incremental learning to add a new image style by learning a new filter bank while holding the auto-encoder fixed. 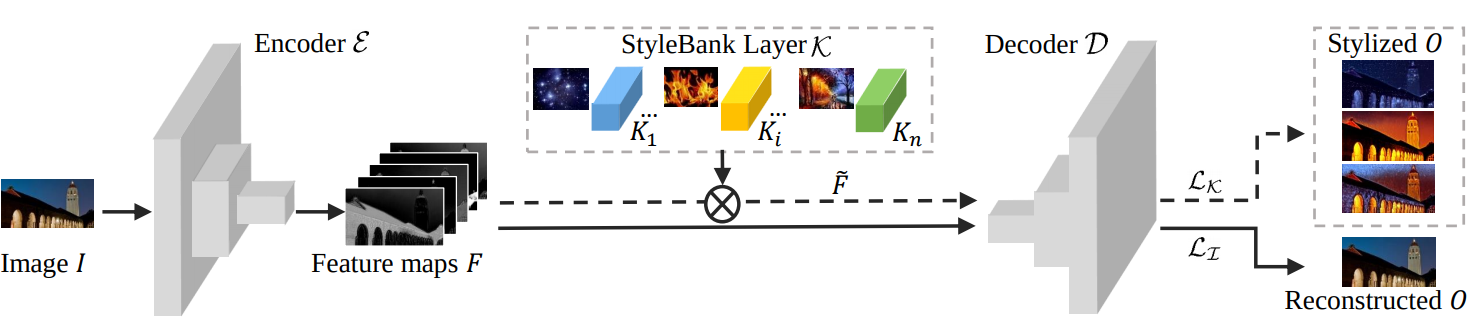Image Source: D Chen et al. ↩

54. Learning Linear Transformations for Fast Image and Video Style Transfer is an approach for universal style transfer that learns the transformation matrix in a data-driven fashion. The method learns two seperate networks to map the covariance metrices of feature activations from the content and style image to seperate metrics. The multiplication of these two metrics is the transformation that maps transfers the distribution of content features to the distribution of the style features. ↩

55. Combining Markov Random Fields and Convolutional Neural Networks for Image Synthesis CNNMRF transfers neural patch from style image to content image. The image below compares the difference between parametric (middle) and non-parametric style transfer. The non-parametric results preseves more miso structure from the style image. Image Source: Combining Markov Random Fields and Convolutional Neural Networks for Image Synthesis, C Li et al. ↩

56. Visual Attribute Transfer through Deep Image Analogy The technique adapts the notion of “image analogy” with features extracted from a Deep Convolutional Neutral Network for matching. A coarse-to-fine strategy is used to compute the nearest-neighbor field for generating the results. It also enforce consistent matching across mutiple layers to remove artifacts in earlier works. Image Source: Visual Attribute Transfer through Deep Image Analogy, J Liao et al. ↩

57. Style Transfer by Relaxed Optimal Transport and Self-Similarity. The authors propose Style Transfer by Relaxed Optimal Transport and Self-Similarity (STROTSS), a new optimization-based style transfer algorithm. Formally, the relaxed EMD is defined as $l_r = max(\frac{1}{n}\sum_{i}\min_{j}C_{ij}, \frac{1}{m}\sum_{j}\min_{i}C_{ij})$, where $C$ is the cost matrix of the distance between pairs of features from the source and the target images. The first term in the bracket computes the sum of shortest distance from the source to the target, and the second term computes the inverse – the shortest distance from target to source. In this way, the match consider both the coverage of the source image and the coverage of the target image. Image Source: Style Transfer by Relaxed Optimal Transport and Self-Similarity, N Kolkin et al. ↩

58. Stable and Controllable Neural Texture Synthesis and Style Transfer Using Histogram Losses The authors first give a mathematical explanation of the source of instabilities in many previous approaches. They then improve these instabilities by using histogram losses to synthesize textures that better statistically match the exemplar. The below image shows the problem of using gram matrix: At left, an example input image, which has a uniform distribution of intensities with a mean of µ1 ≈ 0.707 and a standard deviation of σ1 = 0. At right, an example output image, which has a non-uniform distribution with a mean of µ2 = 1/2 and a standard deviation of σ2 = 1/2. If interpreted as the activation of a feature map with one feature, these two distributions have equivalent non-central second moments of 1/2, and equal Gram matrices. Image Source: Stable and Controllable Neural Texture Synthesis and Style Transfer Using Histogram Losses, E Risser et al. ↩

59. Fast Patch-based Style Transfer of Arbitrary Style The authors propose a feedforward method for style transfer that can be used for arbitrary style images. The encoder in the image below is a pre-trained VGG-19 network. The style swap uses patch matching to replace the feature activations in the content image by the features from the style image. Importantly, the inverse network is trained to invert a deep feature map back to image. The inverse network is trained with real photos, artworks, and pre-computed stylized photos. In this way it can work with arbitary new images in the testing stage. One downside of this method is it still involves patch matching. Although it only needs to do it once in every infernece, it can still be slow. 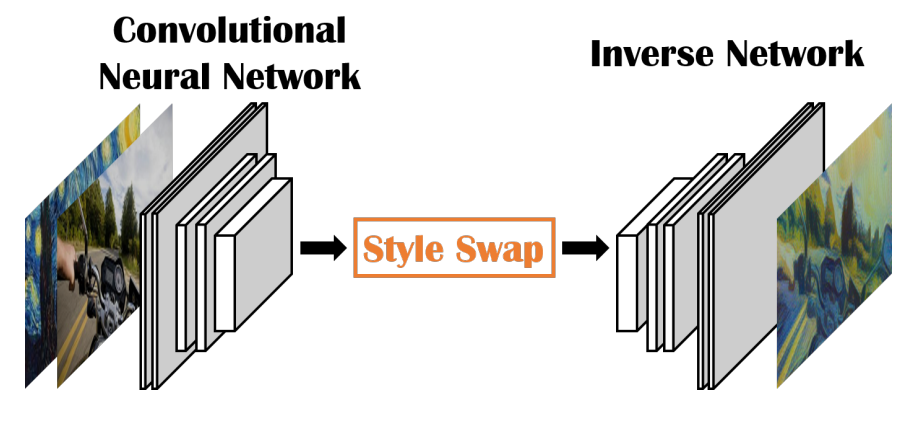Image Source: Fast Patch-based Style Transfer of Arbitrary Style, TQ Chen et al. ↩

60. Precomputed Real-Time Texture Synthesis with Markovian Generative Adversarial Networks The motivation of Markovian (Neural Patches) GANs: real world data does not always comply with a Gaussian distribution (left), but a complex nonlinear manifold (middle). The proposed method adversarially learns a mapping to project contextually related patches to that manifold (right). 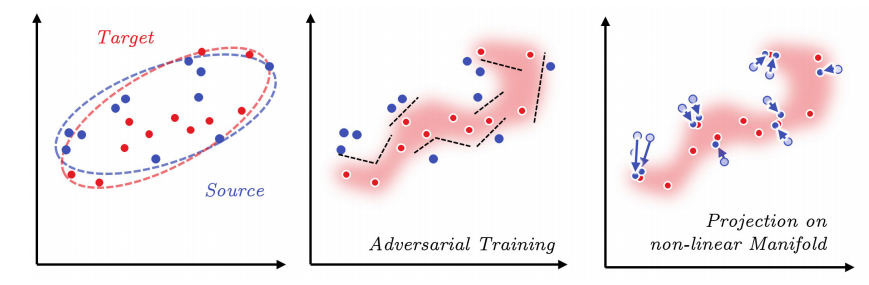Image Source: Precomputed Real-Time Texture Synthesis with Markovian Generative Adversarial Networks, C Li et al. ↩

61. Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks Image-to-image translation is a class of vision and graphics problems where the goal is to learn the mapping between an input image and an output image using a training set of aligned image pairs. However, for many tasks, paired training data will not be available. The authors present an approach for learning to translate an image from a source domain X to a target domain Y in the absence of paired examples. The goal is to learn a mapping $G: X \rightarrow Y$ such that the distribution of images from $G(X)$ is indistinguishable from the distribution Y using an adversarial loss. Because this mapping is highly under-constrained, the authors couple it with an inverse mapping $F: Y \rightarrow X$ and introduce a cycle consistency loss to push $F(G(X)) \approx X$ (and vice versa). Qualitative results are presented on several tasks where paired training data does not exist, including collection style transfer, object transfiguration, season transfer, photo enhancement, etc. The image below shows examples of transfering styles between image and paintings, as well as between images and images. Image Source, Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks, JY Zhu et al. ↩

62. High-Resolution Image Synthesis and Semantic Manipulation with Conditional GANs The authors generate 2048 × 1024 visually appealing results with a novel adversarial loss, as well as new multi-scale generator and discriminator architectures. Furthermore, the authors extend our framework to interactive visual manipulation with two additional features. Below is the network architecture of the generator: a residual network $G_1$ is first trained on lower resolution images. Then, another residual network $G_2$ is appended to $G_1$ and the two networks are trained jointly on high resolution images. Specifically, the input to the residual blocks in $G_2$ is the element-wise sum of the feature map from $G_2$ and the last feature map from G1. 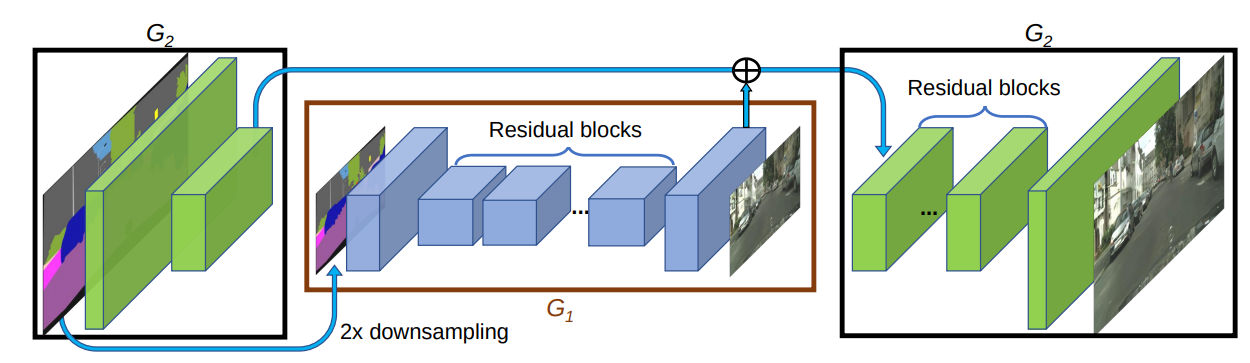Image Source: High-Resolution Image Synthesis and Semantic Manipulation with Conditional GANs, TC Wang et al. ↩